Signification statistique

Qu’est-ce que la signification statistique

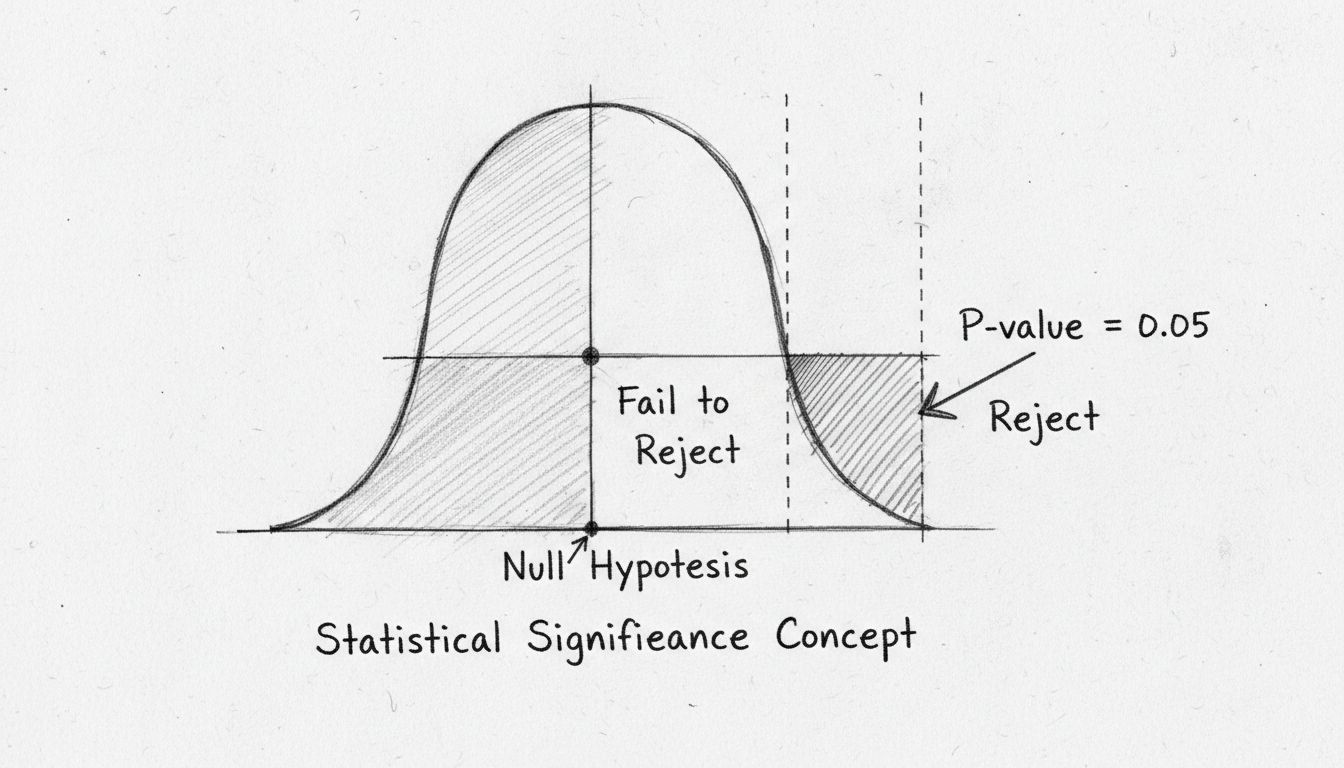
La signification statistique est déterminée par le biais de tests d’hypothèses, une méthode utilisée pour évaluer la plausibilité d’une hypothèse en la comparant à une hypothèse nulle. L’hypothèse nulle stipule généralement qu’il n’y a pas d’effet ou de différence, et l’objectif est de déterminer si les données observées fournissent suffisamment de preuves pour rejeter cette hypothèse au profit d’une hypothèse alternative.

Un résultat est considéré comme statistiquement significatif si la probabilité d’obtenir les données observées, en supposant que l’hypothèse nulle est vraie, est très faible. Cette probabilité est quantifiée à l’aide d’une valeur p. Une valeur p de 0,05 ou moins est couramment utilisée comme seuil de signification statistique, indiquant qu’il y a moins de 5 % de chances que les résultats observés soient dus au hasard.

Composants clés de la signification statistique

1. Valeur p : La valeur p mesure la probabilité d’obtenir des résultats au moins aussi extrêmes que ceux observés, en supposant que l’hypothèse nulle soit vraie. Une valeur p plus faible suggère des preuves plus solides contre l’hypothèse nulle. Le choix du seuil de la valeur p peut varier selon le contexte et le domaine d’étude ; cependant, 0,05 est une norme largement acceptée dans de nombreuses disciplines.
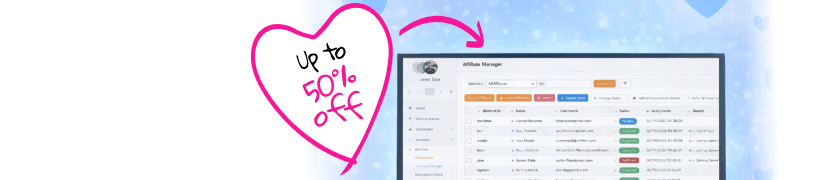
2. Niveau de signification (Alpha) : Il s’agit du seuil fixé par le chercheur avant de réaliser un test. Fixé généralement à 0,05 (5 %), il représente la probabilité de rejeter l’hypothèse nulle alors qu’elle est en réalité vraie (erreur de type I). Les chercheurs choisissent un niveau alpha en fonction du risque acceptable de commettre une erreur de type I, ce qui peut avoir des conséquences sur les décisions politiques ou les conclusions scientifiques.
3. Niveau de confiance : Complémentaire au niveau de signification, il indique le degré de certitude dans les résultats. Un niveau de confiance de 95 % est typique, ce qui implique que si l’expérience était répétée plusieurs fois, les résultats seraient cohérents avec l’effet observé 95 % du temps. Ce niveau de confiance reflète la fréquence à laquelle la vraie valeur du paramètre se situerait dans l’intervalle de confiance si la même population était échantillonnée à plusieurs reprises.

Signification statistique en marketing d’affiliation

En marketing d’affiliation , la signification statistique est cruciale pour évaluer la performance des campagnes marketing, optimiser les taux de conversion et prendre des décisions basées sur les données. Par exemple, lors de tests A/B de différentes pages d’atterrissage ou variantes de messages publicitaires, les marketeurs s’appuient sur la signification statistique pour déterminer quelle version génère le plus de conversions. Ce processus aide à allouer efficacement les ressources et à améliorer le retour sur investissement.

Défis pour atteindre la signification statistique

• Taille d’échantillon : Les petits échantillons peuvent conduire à des résultats peu fiables, car ils ne représentent pas adéquatement la population. Les échantillons plus importants produisent généralement des résultats plus fiables. Cependant, collecter de grands échantillons nécessite aussi plus de ressources et de temps, ce qui rend essentiel de trouver un équilibre entre la taille d’échantillon et les contraintes pratiques.
• Taille d’effet : Elle mesure l’ampleur de la différence entre les groupes. Une petite taille d’effet peut nécessiter un échantillon plus grand pour atteindre la signification statistique. Comprendre la taille d’effet est essentiel pour interpréter les implications pratiques des résultats, car cela donne un contexte sur l’importance des conclusions.
• Comparaisons multiples : Réaliser plusieurs tests augmente le risque d’erreurs de type I. Des ajustements, comme la correction de Bonferroni, peuvent être nécessaires pour préserver l’intégrité des résultats. Lorsqu’on teste plusieurs hypothèses, la probabilité d’obtenir un résultat significatif par hasard augmente, ce qui nécessite des corrections pour prendre en compte ce risque.

Signification pratique vs. statistique

Si la signification statistique indique qu’un effet n’est probablement pas dû au hasard, cela ne signifie pas nécessairement que l’effet est pertinent ou significatif dans des situations réelles. Par exemple, une augmentation du taux de conversion statistiquement significative ne se traduira pas forcément par une hausse substantielle du chiffre d’affaires si la taille de l’effet est faible. La signification pratique considère si l’ampleur de l’effet apporte des bénéfices ou des implications tangibles dans la prise de décision.

Améliorer la signification statistique en marketing d’affiliation

Surveillance continue : Passez régulièrement en revue les données et ajustez les expériences selon l’évolution du marché. Une surveillance continue permet des interventions et optimisations rapides, garantissant l’efficacité des stratégies marketing.

Concevoir soigneusement les expériences : Définissez des hypothèses claires et choisissez des indicateurs appropriés alignés sur les objectifs commerciaux. S’assurer que la conception expérimentale est solide et en accord avec les objectifs permet d’obtenir des informations pertinentes.

Taille d’échantillon adéquate : Veillez à ce que la taille de l’échantillon soit suffisante pour détecter des différences significatives. Calculer la taille d’échantillon nécessaire avant de mener l’étude aide à obtenir une puissance statistique suffisante pour détecter les effets.

Échantillonnage aléatoire : Utilisez des techniques d’échantillonnage aléatoire pour minimiser les biais et garantir que les résultats soient représentatifs du public cible. L’échantillonnage aléatoire améliore la généralisabilité des résultats en réduisant les biais de sélection.

Utiliser des outils analytiques avancés : Utilisez des logiciels statistiques pour calculer précisément les valeurs p et les intervalles de confiance. Ces outils permettent également de visualiser les données et de réaliser des analyses complexes qui seraient difficiles à effectuer manuellement.