Pourquoi la signification statistique est-elle importante ?
Découvrez pourquoi la signification statistique est essentielle dans l’analyse de données, la recherche et la prise de décisions commerciales. Apprenez ce que s...
Découvrez comment la signification statistique permet de déterminer si les résultats sont réels ou dus au hasard. Comprenez les p-values, les tests d’hypothèses et les applications pratiques pour votre entreprise en 2025.
La signification statistique sert à déterminer si un résultat est dû au hasard ou causé par un facteur d'intérêt. Si le résultat est statistiquement significatif, il est peu probable qu'il se soit produit par hasard.
La signification statistique est un concept fondamental de l’analyse de données qui vous aide à distinguer les effets réels des fluctuations aléatoires dans vos données. Lorsque vous réalisez des expériences, des enquêtes ou que vous analysez des indicateurs commerciaux, vous avez besoin d’une méthode fiable pour déterminer si les schémas que vous observez sont réels ou simplement le fruit du hasard. La signification statistique fournit ce cadre critique en utilisant des principes mathématiques pour évaluer la probabilité que vos résultats observés se produisent s’il n’existait réellement aucun effet ou aucune différence entre les groupes que vous comparez.
Le concept est issu des travaux du statisticien Ronald Fisher au début du XXe siècle et est devenu la pierre angulaire des tests d’hypothèses dans presque tous les domaines qui s’appuient sur l’analyse de données. De la recherche pharmaceutique validant de nouveaux traitements à l’optimisation des taux de conversion dans l’e-commerce, la signification statistique fait le lien entre les insights exploitables et les conclusions trompeuses. Comprendre comment fonctionne la signification statistique vous permet de prendre des décisions éclairées, fondées sur des preuves solides plutôt que sur l’intuition ou la coïncidence.
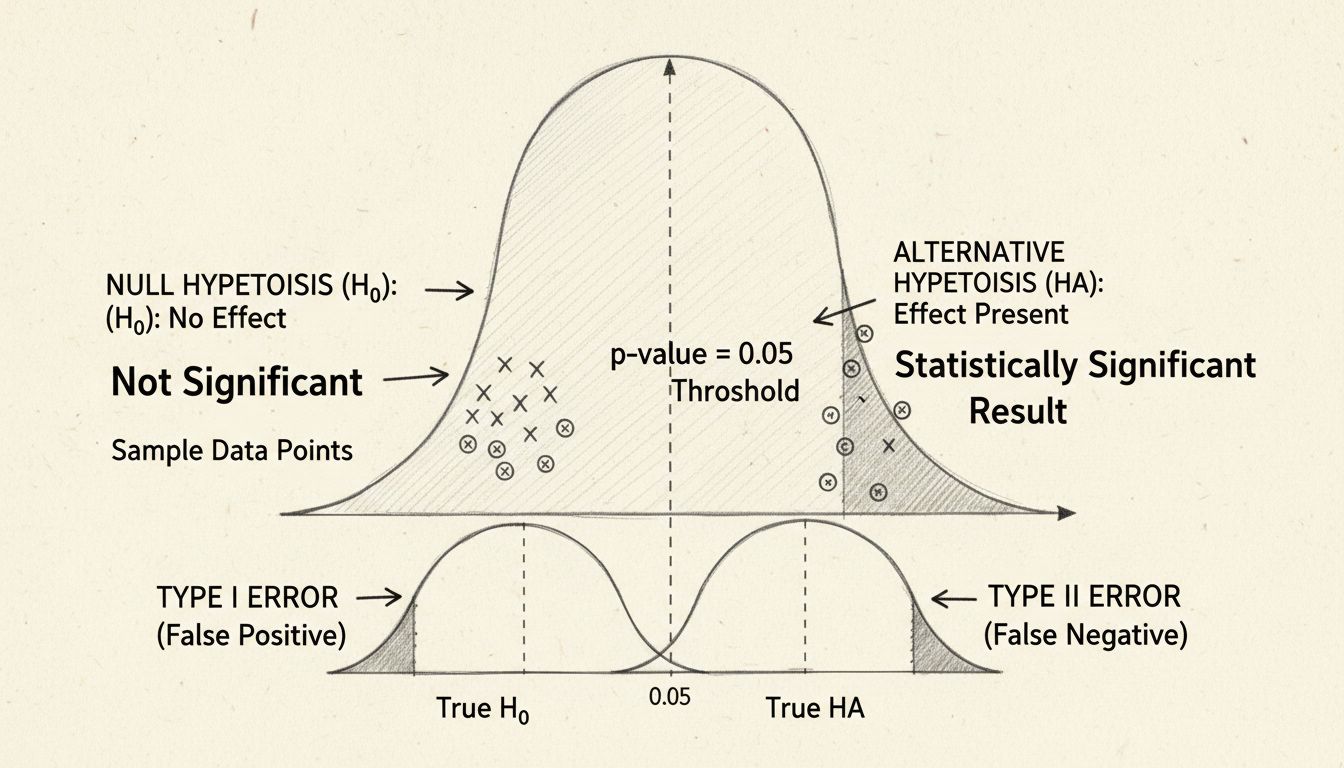
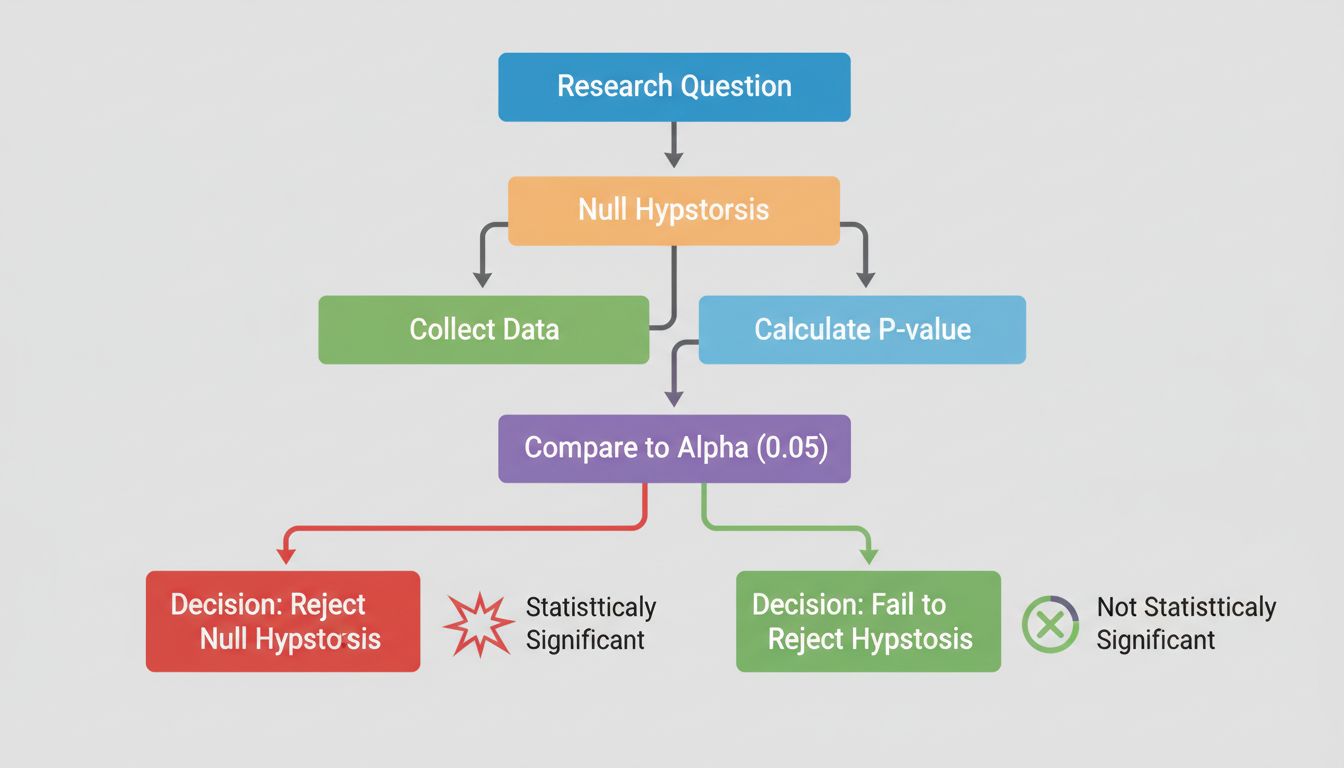
Au cœur de la signification statistique se trouve le test d’hypothèse, une méthodologie structurée pour évaluer les affirmations concernant vos données. Le processus commence par la formulation de deux hypothèses opposées : l’hypothèse nulle et l’hypothèse alternative. L’hypothèse nulle suppose qu’il n’y a pas d’effet réel ou de différence entre les groupes étudiés — elle représente en quelque sorte le statu quo ou l’idée que toute différence observée est purement due au hasard. À l’inverse, l’hypothèse alternative propose qu’il existe un effet ou une différence réelle.
Prenons un exemple concret : vous testez si une nouvelle campagne d’affiliation génère des taux de conversion supérieurs à votre approche actuelle. Votre hypothèse nulle stipulerait que les deux campagnes produisent des taux de conversion identiques, tandis que votre hypothèse alternative affirmerait que la nouvelle campagne fonctionne différemment. Le test statistique évalue alors laquelle des deux hypothèses est la mieux soutenue par les données. Ce cadre évite aux chercheurs et analystes de ne retenir que les résultats qui confirment leurs attentes ; il leur demande de prouver que leurs observations sont peu susceptibles de s’être produites par hasard.
La force du test d’hypothèse réside dans son objectivité. Plutôt que de se fier à un jugement subjectif, vous utilisez des calculs mathématiques pour déterminer si vos données fournissent suffisamment de preuves pour rejeter l’hypothèse nulle. Si les preuves sont suffisamment solides, vous pouvez affirmer avec confiance que votre effet observé est statistiquement significatif — c’est-à-dire qu’il est peu probable qu’il s’agisse d’un coup de chance.
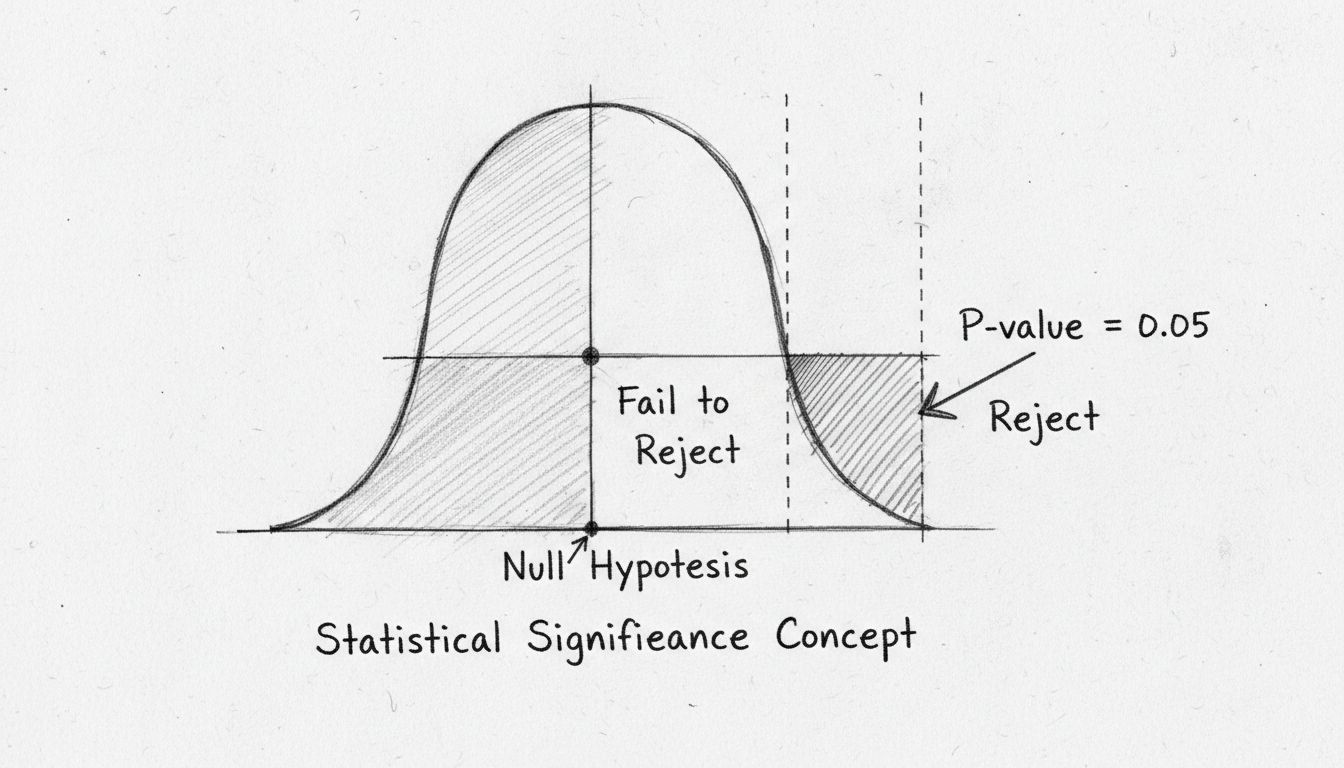
La p-value (valeur p) est sans doute l’indicateur le plus utilisé dans les tests de signification statistique, mais elle est souvent mal comprise. La p-value représente la probabilité d’obtenir vos résultats (ou des résultats encore plus extrêmes) si l’hypothèse nulle était vraie. En d’autres termes, elle répond à la question : « Quelle est la probabilité d’observer ces données s’il n’y avait réellement aucun effet ? » Une petite valeur p indique que vos résultats observés seraient très improbables sous l’hypothèse nulle, suggérant que celle-ci est probablement fausse et que votre effet est réel.
Le seuil conventionnel pour la signification statistique est une p-value inférieure ou égale à 0,05, ce qui correspond à une probabilité de 5 % que vos résultats soient dus au hasard. Cela signifie que vous acceptez un risque de 5 % de rejeter à tort l’hypothèse nulle alors qu’elle est vraie (erreur de type I). Cependant, ce seuil est quelque peu arbitraire et varie selon les domaines et les contextes. En recherche médicale, où les conséquences des faux positifs peuvent être graves, les chercheurs utilisent souvent un seuil plus strict de 0,01 (1 %). À l’inverse, dans la recherche exploratoire ou les tests préliminaires, un seuil de 0,10 (10 %) peut être acceptable.
| Intervalle de p-value | Interprétation | Action typique |
|---|---|---|
| p < 0,01 | Hautement significatif | Forte preuve contre l’hypothèse nulle |
| 0,01 ≤ p < 0,05 | Significatif | Preuve modérée contre l’hypothèse nulle |
| 0,05 ≤ p < 0,10 | Marginalement significatif | Faible preuve contre l’hypothèse nulle |
| p ≥ 0,10 | Non significatif | Preuve insuffisante pour rejeter l’hypothèse nulle |
Il est crucial de comprendre ce que la p-value ne vous dit pas. Une p-value de 0,03 ne signifie pas qu’il y a 97 % de chances que votre hypothèse soit vraie. Elle ne mesure pas non plus la taille ou l’importance pratique de votre effet. Un résultat statistiquement significatif peut tout de même représenter un effet très faible et sans impact réel. Cette distinction entre la signification statistique et la signification pratique est l’une des sources de confusion les plus fréquentes en analyse de données.
Si les p-values vous indiquent si un effet existe, les intervalles de confiance fournissent une information essentielle sur l’ampleur et la précision de cet effet. Un intervalle de confiance est une plage de valeurs qui contient probablement la vraie taille de l’effet, calculée avec un certain niveau de confiance (généralement 95 %). Si vous testez si une nouvelle fonctionnalité d’un programme d’affiliation augmente les commissions, un intervalle de confiance à 95 % pourrait indiquer que l’augmentation réelle se situe entre 2 % et 8 %, avec une certitude de 95 % que la vraie valeur est dans cet intervalle.
Les intervalles de confiance offrent plusieurs avantages par rapport aux seules p-values. D’abord, ils communiquent à la fois la direction et la magnitude d’un effet, vous donnant une vision plus complète de vos résultats. Ensuite, ils aident à évaluer la signification pratique — même si un effet est statistiquement significatif, si l’intervalle de confiance montre que l’effet est négligeable, sa mise en œuvre peut ne pas être justifiée. Enfin, des intervalles étroits indiquent des estimations précises, tandis que des intervalles larges révèlent une plus grande incertitude.
La taille d’effet mesure la force de la relation entre les variables ou l’ampleur de la différence entre les groupes. Parmi les mesures courantes, on trouve le d de Cohen (pour comparer des moyennes), les coefficients de corrélation et les rapports de cotes. Un effet peut être statistiquement significatif mais avoir une faible taille d’effet, donc un impact pratique minime. À l’inverse, un effet important peut ne pas atteindre la signification statistique si l’échantillon est trop petit. Les analystes professionnels rapportent toujours la taille d’effet en plus des p-values pour donner une vision complète de leurs résultats.
La taille de l’échantillon joue un rôle crucial dans la détermination de la signification statistique. Des échantillons plus grands donnent plus d’informations sur votre population et réduisent l’impact de la variation aléatoire, ce qui facilite la détection d’effets réels. À l’inverse, de petits échantillons sont plus sensibles aux fluctuations aléatoires, ce qui peut conduire à des faux positifs (détection d’un effet inexistant) ou à des faux négatifs (non-détection d’un effet réel).
La relation entre la taille d’échantillon et la puissance statistique est fondamentale dans la conception d’une étude. La puissance statistique est la probabilité de rejeter correctement l’hypothèse nulle lorsqu’elle est fausse — autrement dit, votre capacité à détecter un effet réel. La plupart des chercheurs visent une puissance de 0,80 (80 %), acceptant donc un risque de 20 % de manquer un effet réel. Pour atteindre ce niveau, il faut une taille d’échantillon suffisante, qui dépend de la taille d’effet attendue, du seuil de signification choisi et du type de test statistique utilisé.
Avant de mener une étude ou une expérience, il est recommandé de réaliser une analyse de puissance pour déterminer la taille d’échantillon requise. Cela évite de gaspiller des ressources sur des études trop petites pour détecter des effets significatifs, tout en évitant des études inutilement grandes et coûteuses. Dans le contexte de l’affiliation, cela signifie déterminer combien de conversions ou de clics doivent être observés avant de pouvoir conclure avec certitude qu’un changement de campagne a un impact réel.
Les différentes questions de recherche et types de données requièrent des tests statistiques adaptés. Le choix du test dépend du nombre de groupes comparés, de la distribution des données, du caractère indépendant ou apparié des échantillons, et du type de variable mesurée (continue, catégorielle, etc.).
Le test t de Student compare les moyennes de deux groupes et est l’un des tests les plus utilisés. Il convient pour des données continues (comme des montants de chiffre d’affaires) et permet de déterminer si deux groupes diffèrent significativement. Le test prend en compte la variabilité au sein de chaque groupe et la taille des échantillons, produisant une statistique t à comparer à une valeur critique pour juger de la signification.
Le test du khi carré (Chi-squared) est utilisé pour des données catégorielles afin de déterminer si les fréquences observées diffèrent significativement des fréquences attendues. Si vous analysez si le canal d’affiliation (email, réseaux sociaux, bannières) influence les taux de conversion, ce test est approprié.
L’ANOVA (Analyse de la variance) généralise le test t à la comparaison de moyennes entre trois groupes ou plus. Cela évite le problème des comparaisons multiples, où effectuer de nombreux tests séparés augmente la probabilité de faux positifs.
Les tests de Mann-Whitney U et Wilcoxon rank-sum sont des alternatives non paramétriques utilisées lorsque les données ne remplissent pas les conditions des tests paramétriques, par exemple quand elles ne suivent pas une distribution normale.
Dans le monde des affaires, la signification statistique guide la prise de décisions critiques dans de nombreuses fonctions. Les équipes marketing utilisent les tests A/B et la signification statistique pour déterminer si les modifications de site web, d’objet d’email ou de créations publicitaires améliorent effectivement les performances. Plutôt que de se fier à l’intuition ou à des observations ponctuelles, les entreprises data-driven fixent des seuils de signification avant de lancer les tests, garantissant des décisions fondées sur des preuves fiables.
Dans l’affiliation, la signification statistique permet d’identifier quels affiliés, campagnes et stratégies promotionnelles génèrent réellement du chiffre d’affaires, par opposition à ceux qui semblent performants par simple hasard. Lorsque vous évaluez si une nouvelle structure de commission augmente la performance, les tests statistiques vous évitent de prendre des décisions coûteuses basées sur des fluctuations de court terme. La plateforme analytique avancée de PostAffiliatePro vous permet de suivre les métriques affiliés avec la rigueur statistique nécessaire pour des optimisations en toute confiance.
En recherche pharmaceutique et médicale, la signification statistique détermine si de nouveaux traitements sont suffisamment efficaces pour être approuvés et utilisés. Les essais cliniques doivent démontrer que les bénéfices d’un médicament sont statistiquement significatifs avant d’être prescrits aux patients. Les enjeux sont majeurs, c’est pourquoi la recherche médicale utilise généralement des seuils de signification plus stricts que d’autres domaines.
L’une des idées reçues les plus répandues est que la signification statistique prouve la causalité. Une corrélation statistiquement significative entre deux variables ne signifie pas que l’une cause l’autre. L’exemple classique est la forte corrélation entre les sorties de films avec Nicolas Cage et les noyades dans les piscines — évidemment, l’un ne cause pas l’autre. La signification statistique indique seulement qu’une relation est peu probable d’être due au hasard ; prouver la causalité nécessite d’autres preuves, comme un mécanisme logique, l’ordre temporel et des expériences contrôlées.
Une autre erreur fréquente est le p-hacking ou data dredging, qui consiste à multiplier les tests statistiques sur le même jeu de données jusqu’à trouver des résultats significatifs. Cette pratique augmente artificiellement la probabilité de faux positifs, car en multipliant les tests, on finit par trouver un résultat significatif par simple hasard. Si vous effectuez 20 tests indépendants à un seuil de 0,05, vous vous attendez à trouver environ un faux positif juste par hasard. Les chercheurs responsables spécifient à l’avance leurs hypothèses et tests statistiques, évitant ce problème.
Mal interpréter les résultats non significatifs est également un écueil courant. Un résultat non significatif ne prouve pas qu’aucun effet n’existe ; il signifie simplement que vous ne disposez pas de suffisamment de preuves pour rejeter l’hypothèse nulle. Cela peut être dû à une taille d’échantillon insuffisante, une forte variabilité des données, ou à l’absence réelle d’effet. L’absence de preuve n’est pas la preuve de l’absence.
Le domaine de la statistique continue d’évoluer, avec une prise de conscience croissante des limites de l’approche traditionnelle centrée sur la p-value. De nombreux statisticiens prônent désormais une approche plus nuancée combinant p-values, tailles d’effet, intervalles de confiance et méthodes bayésiennes. Les statistiques bayésiennes, qui intègrent les connaissances antérieures et mettent à jour les croyances en fonction des données observées, offrent un cadre alternatif jugé par certains plus intuitif et flexible que l’approche fréquentiste.
Les tests séquentiels et les plans adaptatifs gagnent en popularité, permettant aux chercheurs de surveiller les résultats au fil de l’accumulation des données et de décider de poursuivre, modifier ou arrêter les études en fonction d’analyses intermédiaires. Cette approche est particulièrement précieuse en entreprise, où les décisions doivent être prises rapidement. Des outils comme Statsig’s Stats Engine mettent en œuvre des tests séquentiels avec contrôle du taux de fausses découvertes, permettant des décisions plus rapides et plus précises lors des expérimentations.
La crise de la reproductibilité en science a également mis en lumière l’importance de bien comprendre la signification statistique. De nombreux résultats publiés ne sont pas reproductibles, en partie parce que chercheurs et revues se sont focalisés sur l’obtention de la signification statistique, au détriment de la taille d’effet et de la signification pratique. L’avenir s’oriente vers plus de transparence, la pré-inscription des études et la publication de tous les résultats, qu’ils soient significatifs ou non.
Pour utiliser efficacement la signification statistique, définissez à l’avance votre seuil de signification et la taille d’échantillon requise avant d’analyser vos données. Cela évite la tentation d’ajuster les seuils après avoir vu les résultats. Rapportez toujours la taille d’effet et les intervalles de confiance en plus des p-values pour donner une vision complète de vos résultats. Évaluez la signification pratique de vos résultats — un effet statistiquement significatif peut être trop faible pour avoir un intérêt concret.
Soyez transparent sur votre méthodologie, notamment sur la gestion des données manquantes, des valeurs aberrantes et des comparaisons multiples. Si vous avez effectué plusieurs tests, appliquez les corrections appropriées comme la correction de Bonferroni pour maintenir votre niveau global de signification. Documentez votre processus d’analyse et soyez prêt à partager vos données et vos scripts pour vérification et reproduction.
Enfin, rappelez-vous que la signification statistique est un outil, pas une finalité. Elle vous aide à prendre de meilleures décisions en réduisant l’influence du hasard, mais doit être associée à l’expertise métier, à la prise en compte du contexte et au jugement professionnel. En affiliation, la signification statistique vous aide à identifier les stratégies réellement performantes, mais tenez aussi compte des coûts d’implémentation, de la satisfaction des affiliés et de la pérennité à long terme dans vos choix stratégiques.
Les outils avancés d’analyse et de reporting de PostAffiliatePro vous aident à suivre la performance de vos affiliés avec une rigueur statistique. Identifiez quelles campagnes génèrent réellement des résultats et optimisez votre programme d’affiliation sur la base de données fiables.

Découvrez pourquoi la signification statistique est essentielle dans l’analyse de données, la recherche et la prise de décisions commerciales. Apprenez ce que s...
La signification statistique exprime la fiabilité des données mesurées, aidant les entreprises à distinguer les effets réels du hasard et à prendre des décision...
Maîtrisez la signification statistique dans les tests A/B pour les campagnes d'affiliation aux paris.
Consentement aux Cookies
Nous utilisons des cookies pour améliorer votre expérience de navigation et analyser notre trafic. See our privacy policy.